Conway's Game of Life in MATLAB
I'm fairly sure the first place I heard about Conway's Game of Life was the Numberphile video with John Conway himself talking about his cellular automaton.
For some background, Life uses a grid of cells that are in one of two states, live or dead, and applies a simple set of rules to this grid to determine which cells are live in the next generation. Conway's intention was to develop a simple set of rules that allowed complex behaviours to emerge over time. Conway came up with four rules [1]:
- Any live cell with fewer than two live neighbours dies (referred to as underpopulation or exposure).
- Any live cell with more than three live neighbours dies (referred to as overpopulation or overcrowding).
- Any live cell with two or three live neighbours lives, unchanged, to the next generation.
- Any dead cell with exactly three live neighbours will come to life.
publish function to turn my script directly into nicely-formatted HTML, so I'll be explaining the code in the order it ended up, not the order it was written. Not having all the previous versions around to explain the process is a little annoying, so I think I might learn git at some point to help with archiving work as I go.GameOfLife.m
%GameOfLife % An implementation of Conway's Game of Life in MATLAB % Rob Cook, 2021 clear close all
Clearing and closing everything is probably slightly overkill - it's certainly possible to get this to run without this but making sure MATLAB isn't doing anything else makes debugging a whole lot easier.
Input dialog box
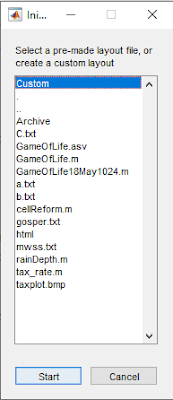
The first thing the user interacts with is the dialog box asking them whether they want to use a custom layout (one they will input to the grid using the cursor) or load one in from file. The file format used here is .txt, with the cell encoding taken from conwaylife.com, which is a wiki with plenty of resources on the many variations on Life. These files have 'O' (note that's the character O, not the number 0) for live cells and '.' for empty ones. The advatange of handling this file type is that I didn't need to program loads of different layouts by hand, but they have an odd format, with inconsistent numbers of characters in each row, with only the number required to show all the live cells being included. Handling this variable row length was a good challenge - but I'll discuss that when the relevant code turns up.
% Dialog text prompt = {'Select a pre-made layout file, or create a custom layout',''}; % Dialog title dlgtitle = 'Initial condition selection'; % List files in current directory d = dir; % Options are custom layout or files in directory optList = {'Custom',d.name}; inputFile = listdlg('PromptString',prompt,'Name',dlgtitle,... 'SelectionMode','single','OKString','Start','ListString',optList);
MATLAB simply reads the current directory files to provide the list of available files to load, which was easy to code but obviously doesn't remove incompatible file types from the list. Selecting one of these trhow s an error
pretty quickly so this isn't a huge problem, but it's something I'd work on more if the code were for anything more than my own amusement. Appending Custom to the start of the list (as opposed to the end) makes
it more visible to the user, and the default option.
Create the play area
% The area will be a gSize x gSize grid gSize = 50; % Pad to avoid out-of-range array indices and hide edge case errors pad = 10; % The calcs will be done on a grid which is padded calcSize = 2*pad+gSize; % Create corresponding logical array isLive = false(calcSize); % Set up plot window figure(1) set(gcf,'position',[500,400,550,500]) grid on axis([pad gSize+pad pad gSize+pad]) axis square hold on % Set tick locations ticklocs = (pad:1:gSize+pad); xticks(ticklocs) yticks(ticklocs) % Hide tick labels set(gca,'Yticklabel',[]) set(gca,'Xticklabel',[])

The grid created here really isn't a very exciting plot, but the code to create it has some elements to note. Most importantly, this is the first time the pad
value is used. This padding is necessary to prevent 1) the code from crashing due to out-of-range array indices, and 2) to prevent the edge cases from being displayed on the
plotted grid. In theory, Life should be run on an infinite field, but that's hard, so I'm cheating a lot and just having it run on a 70-by-70 grid, from which I sample
the centre 50x50 to be shown. This is a bodge, certainly, but it works quite nicely - it's rare for the edge cases to build up enough to encroach on the visible play area.
For custom layouts
If the user selects Custom then this section of code runs. Here we see a second reason for having 'Custom' be the first option, as it allows us to use inputFile == 1
to check if a custom layout is requested, rather than anything more complex involving enumerating the options in the dialog.
if inputFile == 1
The loop runs until broken by the user clicking outside of the input area. Initially I tried using a button in the plot window, but because MATLAB doesn't really have interrupts,
it was not very reliable - the code would get back to the ginput phase without registering the button press, therby not ending the loop. Using an out-of-bounds click
as the endpoint is useful because it automatically breaks ginput. When I was struggling with getting the end button to behave, I'd already written the if
statement that handles out-of-area input, because it was causing out-of-range array indices. Adding a break made it exit the loop exactly as required.
For points that lie within the play area, we then check if the point is currently set to 'false', which I've used in the logical array to denote an empty cell. Empty cells are then filled, both by setting the logical location to 'true' and by drawing a yellow square in the appropriate cell in the plot window. The square drawn is given a handle to allow us to refer back to it. If the cell was live, it's emptied and the graphics object related to the logicla cell is deleted. Using graphics handles in this way saves drawing over existing objects, or having to find indices - a pleasingly elegant solution.
% Set index i = 1; % Set loop to run continuously inputPhase = true; while inputPhase == true % Title provides instructions to user title('Click in cells to set them to live; click anywhere else to end input'); % Take 1 clicked location [x(i),y(i)] = ginput(1); % Click locations are rounded up to provide top-right corner location x(i) = ceil(x(i)); y(i) = ceil(y(i)); % Handle out-of-bounds input if x(i)<=pad||y(i)<=pad||x(i)>gSize+pad||y(i)>gSize+pad % Delete out-of-bounds entry x(i) = [ ]; y(i) = [ ]; % Reduce index by 1 to prevent 0 in arrays i = i-1; % End input phase break % Make dead cell live elseif isLive(x(i),y(i)) == false % Fill cell hCell(i) = fill([x(i)-1 x(i)-1 x(i) x(i)],... [y(i)-1 y(i) y(i), y(i)-1],'y'); % Record location of fill object handle gHandle(x(i),y(i)) = i; % Set logical cell to live isLive(x(i),y(i)) = true; % Revert cell to dead if live else % Delete the live cell delete(hCell(gHandle(x(i),y(i)))) % Set logical cell to dead isLive(x(i),y(i)) = false; end % Increment index i = i+1; end
The key output of this section in isLive, a logical array of all the currently live cells. This will be used throughout the program to keep track of the cell states.
For layout loaded from file
Loading a layout from file uses the cellReform function, at the end of the code. The output from that is then converted from a set of linear indices to cartesian
coordinates. As I wrote this post, I realised that this could have been moved into the function, or the function added to the main code. The only reason it was separate in the first
place was to facilitate debugging, as processing the file became a little fiddly.
numLive is used to keep track of the number of live cells, which is needed because the cell locations are stored as cartesian coordinates, rather than using the logical
to track tehm the whole time. It also allows the code to break when the number of live cells reaches 0, which avoid the user having to stare at a blank plot.
else % Use cellReform function to process file isLive = cellReform(optList(inputFile),calcSize); % Find locations of live cells [x,y] = ind2sub([calcSize,calcSize],find(isLive)); % Update number of live cells numLive = sum(isLive,'all'); % Plot cells for i = 1:numLive fill([x(i)-1 x(i)-1 x(i) x(i)],[y(i)-1 y(i) y(i) y(i)-1],'y') end end
Here we have the output of loading the Gosper Glider Gun file, plotted nicely in the centre of the play field. Now all we need to do is a bit of cleanup, and then apply the rules to iterate the generations.

Finish setup
The first thing I do here is count the live cells, making the time I just did that in the previous section redundant - probably should have caught that one, but it doesn't break anything, and the impact on the speed of the code is negligible.
The code then checks that there is a non-zero number of cells to apply the rules to, and makes a stop button to halt the program. I thought about making some more involved code to detect
states where the program should halt, e.g. if no change is detected in isLive for a few generations, but felt that it would probably introduce some edge cases and errors that
were best avoided, not least because the program would need to keep track of multiple iterations of isLive. Let's say I've left writing that as an exercise for the reader.
% Count live cells numLive = sum(isLive,'all'); % If there are no live cells, then end the program if numLive ==0 error('No live cells remaining'); end % Create button to allow user to stop program finishButton = uicontrol('Style', 'PushButton', ... 'String', 'Finish',... 'Callback', 'delete(finishButton)'); title('Generation 1. Press any key to continue.') % Pause to display initial config pause;
The pause here was a later addition, so that the user could sit and look at the intial conditions of the layout for as long as necessary. This is more relevant for layouts from file,
because the user might not know what these look like.

Loop through generations
Now we come to the loop that applies the rules. This forms the bulk of the code and while not that tricky to write, it did require a bit of thought to get the order of operations optimised. Here the loop's been set to run 100 times, but this is arbitrary, and I think for a more developed version I'd look to either allow the user to set this before they start, or leave it as an infinite loop, broken only by the 'Finish' button.
for loop = 1:100
Left to run at full speed the generations pass so fast that it's a bit tricky to see what's happening, so I introduced a delay term. While a simple fixed delay would probably have been sufficient, the time taken for generation does vary a bit based on the number of live cells that need to be accounted for, so I decided to implement a variable delay that times the loop and then pauses for long enough for the user to see what's happening. Again, allowing the user to tune this (potentially on-the-fly) would be a nice bonus, but the 0.1s I've used is about the right speed to show the genrations as a smooth animation.
% Add generation info to title
title(strcat('Generation:',num2str(loop+1)))
% Finish sim on button press
if ~ishandle(finishButton)
break;
end
drawnow;
% Adaptive loop delay: Pause to allow user to see generations
% proceeding if code is running quickly (avoids slowing down larger
% systems unnecesarily)
loopTime = toc;
delayTime = 0.1;
if loopTime < delayTime
pause(delayTime-loopTime)
end
% tic for adaptive loop delay
tic



Count the neighbours of each cell
The rules of Life use two pieces of information - whether or not any given cell is live (which we already have stored in isLive) and the number of live neighbours any given cell has.
This second value is calculated here. The benefit of having the live locations stored as coordinates (rather than just using the logical array of isLive) is shown here, as it makes it easier
to address each live cell to find its neighbours. This avoids either having to loop over all the cells, live or not, to calculate the number of neighbours each has (which would be slow), or having to come
up with a vectorised version of this loop which could run the calculation in parallel.
The loop here simply adds 1 to a 3x3 square centred on each live cell, then subtracts 1 from the cell itself (the cell doesn't count as its own neighbour).
This neighbours array will then be processed to apply the rules and work out which cells are live in the next generation.
% Set neighbour matrix to 0, with padding rows&cols for edge cases
neighbours = zeros(calcSize);
% Loop through all live cells
for i = 1:numLive
% Add 1 to all their neighbours
neighbours(x(i)-1:x(i)+1,y(i)-1:y(i)+1) = ...
neighbours(x(i)-1:x(i)+1,y(i)-1:y(i)+1) + 1;
% Subtract 1 from live cells themselves
neighbours(x(i),y(i)) = neighbours(x(i),y(i))-1;
end
Apply Conway's rules
After this has been done for all live cells, we apply the game rules in a simple fashion, working on the entire logical array in parallel, which is
faster (and cleaner) than looping over all the elements.
The edge cases of the play space are handled here, by making all the edge cells of the 70x70 grid empty using the padarray function.
This is a really handy tool in MATLAB, and saves a lot of messing about with finding the edges of an array.
% Cells with 3 neighbours will all be live
nextGenLive = neighbours == 3;
% Cells with 2 neighbours will only be live if they are currently live
nextGenLive = nextGenLive + (neighbours==2 & isLive);
% Update live cells
% To prevent out-of-bounds indices, no edge cell is live
isLive = padarray(nextGenLive(2:end-1,2:end-1),[1,1]);
Update plot
The plot is updated, showing our new state:

We also run some basic reset code, that gets us back to the state we need to enter the loop: converting to cartesian coordinates, updating numLive
and ending the code if we're out of live cells.
% Delete previous cells from plot cla % Find x y locations of live cells [x,y] = ind2sub([calcSize,calcSize],find(isLive)); % Update number of live cells numLive = sum(isLive,'all'); % End if no live cells if numLive == 0 error('No live cells remaining') end % Plot cells as squares for i = 1:numLive fill([x(i)-1 x(i)-1 x(i) x(i)],[y(i)-1 y(i) y(i) y(i)-1],'y') end
end
The cellReform function
This function takes the .txt files from ConwayLife.com and reformats them to the logical array needed in this program.
The first stage in this is importing the file the user has selected, which comes in as an array of cells, each containing
the characters describing one row of the array. The number of cells (and therefore rows) is stored as rowN.
The largest number of characters in any of these cells tells us the size of longest row in the grid (rowL), which is
then fed into a cell function, which pads out each row to the length of the longest one, evening them out. This cell
function was one of the trickiest bits of code to debug, and it took looking at several different MATLAB forum posts to get it right.
The array of cells is then converted into a matrix to be padded up to 70x70.
Padding is done by halving the difference between the calculated grid size (70x70) and the dimensions of the loaded file and using
ceil to get an integer. The locations of the live cells in the loaded file are then transferred to an empty matrix of the right size.
function [output] = cellReform(fileName, calcSize) %cellReform reformats cell data to Matlab boolean % Takes cell data (in .txt) from conwaylife.com and converts it to a % MATLAB boolean to be loaded into GameOfLife.m. Layouts smaller than % gSize x gSize will be padded to centre them. % Load file as strings to find number of rows input = importdata(char(fileName)); [rowN,~] = size(input); % Find longest row using cellfun (input rows not all equal) rowL = max(cellfun('length',input)); % Pad cells to even out row lengths input = cellfun(@(x) ([x zeros(1, rowL - length(x))]),input,'un',0); % Convert to matrix form input = cell2mat(input); % Error if provided layout is too big if rowN>calcSize||rowL>calcSize error('Layout too large for grid. Alter gSize.') end % Find indices of live cells in array liveLocs = input == 'O'; % Pad provided layout to fit gSize % Find vertical padding req vPad = ceil((calcSize-rowN)/2); % Find horizontal padding req hPad = ceil((calcSize-rowL)/2); % Position the file's cells within the larger grid output = zeros(calcSize); output(hPad+1:hPad+rowL,vPad+1:vPad+rowN) = liveLocs'; % Debug % imshow(output, 'InitialMagnification',800); end
I really enjoyed this project - I did it over a series of evenings around the time I finished up my master's thesis, and was a welcome distraction from that work. It contained some challenges I hadn't thought about before, and gave me quite a pleasing result, even if it isn't very polished. I've already mentioned some features that it would benefit from, and I'm sure there are more things I could do to optimise it, but I'm happy to put this one down for now - I might port it into another language at some point, and improve it then.
Have any thoughts about this post? Use the contact page to get in touch.